Codeforces Round #703 (Div. 2) A ~ F题解

快乐补题场

A. Shifting Stacks

很显然，让原序列排成0,1,2,3,...的形式能让后面的选择更优。复杂度 $O(Tn)$ 。

B. Eastern Exhibition

x，y明显可以分开来考虑。

那么先看两个点x1,x2（简记x1 < x2）的情况：

可以发现 $[x1,x2]$ 的点都能用来作为博物馆。

对于多个点来说，考虑每次匹配最外侧两个点。

对于偶数点来说，最内侧的两个点即为取值范围；

对于奇数点来说，最内侧的一个点即为取值范围。

初中数学题：）

C Guessing the Greatest

easy 版本：查询40次。

查一次全局，找到次大的位置x。如果在左区间，查一次左区间，有两种结果：还是x，那么最大值必在左区间，否则必在右区间。反之，一样的道理。每次查询两次，可以把空间缩小一倍。

hard 版本：查询20次。

查一次全局，找到次大的位置x。首先查一次 [1,x] （x=1时不用查） 看最大值在x左还是x右。举例最大值在x右，那么 l = x + 1,r = n，每次查 [x,mid] 就能判断最大值在哪个位置，即区间单调缩小。复杂度 $O(\log n)$ 。

D. Max Median

找全局最大中位数。

找中位数必定需要排序。这里利用了 01序列 排序可以做到 $O(1 \sim \log n)$ （ $O(1)$ 是静态排序，即用前缀和来判定， $O(\log n)$ 则是线段树动态维护，区间统计 & 区间覆盖） 。那么枚举答案 x ，当 $a_i \geq x$ 该位置 $b_i$ 为1，否则为-1。那么只要满足一个区间 $\sum\limits_{i=l}^r b_i > 0$ ，那就证明该区间的中位数大于等于枚举的答案。

复杂度 $O(n\log n)$ 。

E. Paired Payment

每次只能走两步，每两步产生的代价为 $(d_1 + d_2)^2$ 。

记录上次经过的边的边权。那么每个点的状态得扩成边权权值的大小，所幸边权大小 <=50 。那么上次经过边的边权为0，说明下一步是奇数步，否则是偶数步（由于边权 >0 ）。

复杂度 $O(\max{w} n\log n)$ 。

F. Pairs of Paths

听说是经典结论：对于有根树，树上两条路径若有交（至少一个交点），那么一条路径的lca必然在交集内。具体地，是两条路径lca中较深的一个。

那么枚举每个树点，作为两路径较深的交点。

实际统计时，发现直接统计仅交一个点的难求。那么就统计所有相交方案，再减去至少交2个点的方案数，分类讨论出所有情况。

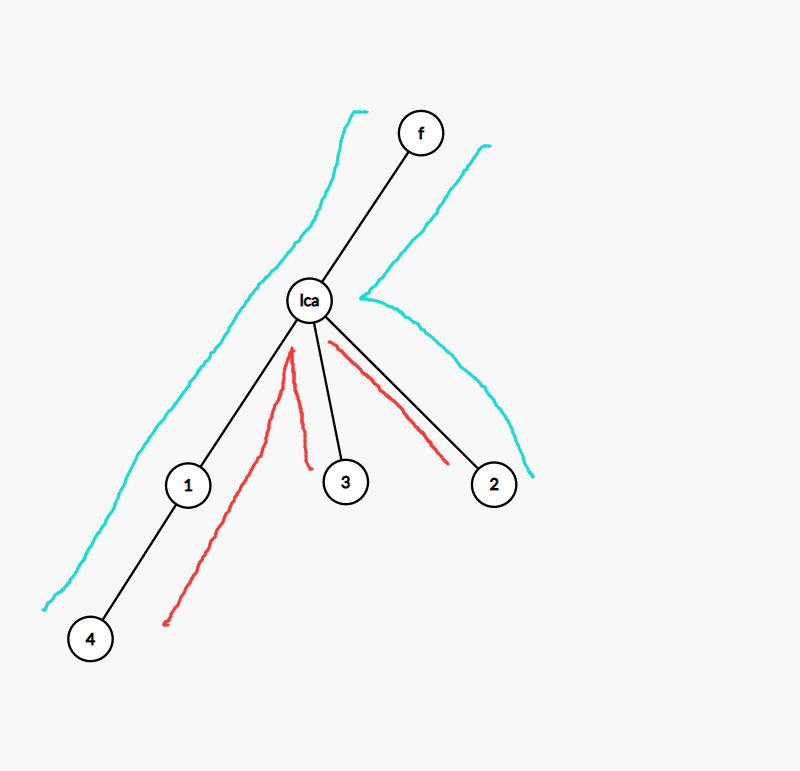
设当前枚举的lca为z。图中蓝色路径跨过z，红色路径以z为lca。那么每枚举一个z，就新增了路径相交方案数 过z蓝线 * 红线 + 红线两两匹配。对于过z的蓝线，由于只查询一次，故路径覆盖用树上差分， $O(n+m)$ 搞一波。此时设蓝线数为 d[z] 。

然后就分类讨论红线内部相交超过2的情况，与红线与蓝线相交超过2的情况，乱搞一下就行。