Codeforces Round #705 (Div. 2) A ~ F 题解

A. Anti-knapsack

有数 [1,n] 和 k ，问最大集使任意子集的和均不为 k 。

[k+1,n] 的自然在集合内。$[k-1,\lceil \frac{k}{2}\rceil]$ 可以选。发现没有比这个更大的区间了。有兴趣再看tutorial。。

B. Planet Lapituletti

暴力移时间，翻转判断即可。

C. K-beautiful Strings

找一个比当前串s字典序大的，第一个满足里面字符出现个数均能被 k 整除的字符串。

首先 n 整除不了 k 的不行，否则都有解 （串zzz...）。对于相对的字典序问题，套路枚举前面有 i - 1 位不动，第 i 位动能否成立的问题。

然后瞎搞搞就好。注意第 i 位的字符要大于原第 i 位字符。

D. GCD of an Array

这题直接对于每个位置维护质因子的个数即可。当全局某质因数都出现过，即 cnt[p] = n ，才纳入全局gcd统计。

复杂度 $O(n\log^2n)$ ，这个界很松。。

E. Enormous XOR

首先可以确定的是，当 r,l 的最高位不同时，可以通过构造

$\begin{aligned} 1000\dots 00 \\ 111\dots 11 \end{aligned}$

来实现异或最大值。

当 r,l 最高位相同时，根据异或前缀和的公式：

$\begin{aligned} & xor_i = i , i \bmod 4 = 0 \\ & xor_i = 1 , i \bmod 4 = 1 \\ & xor_i = i + 1, i \bmod 4 = 2 \\ & xor_i = 0, i \bmod 4 = 3 \end{aligned}$

可知对于答案区间 $xor_j \oplus xor_{i - 1}$ ，最佳的选法即为最大的 $xor_j$ ，搭配一个较好的 $xor_{i-1}$ ，分类讨论一下就求出来了。

F. Enchanted Matrix

设一个矩阵能分成若干相同的 $(r,c)$ 记作 $q(r,c)$ 。那么等价于 q(r,m) \and q(n,c) 。这个充要性比较好证，利用了子矩阵的自相似性。

那么问题就分成了行列两个独立的子问题。

这里有个很有趣的结论。若一段区间可以分别分成 k1,k2 份，每份两两相同，那么也可以分成 $\operatorname{lcm}(k1,k2)$ 份。可以发现，当 $k1,k2$ 互质， $\operatorname{lcm}(k1,k2) = k1 * k2$ 。那么如果 $k1,k2,\dots$ 分别是质因子的幂形式，得到的累乘形式也是不同的，即质因子之间独立。

那么只需要知道每个质因子 $p_i$ 能分成 $p_i^{c_i}$ 份，那么一共有 $\prod (c_i + 1)$ 种选法。

那么对于能分成 $k$ 份，怎么通过查询两次来确定区间 k 等分呢？

当 k 等于 2 时，只需要查询左右两个区间，递归往下找就行了（利用自相似性）

当 k 为其他质因子时，可知区间定被分为奇数个区间，此时可以这么查

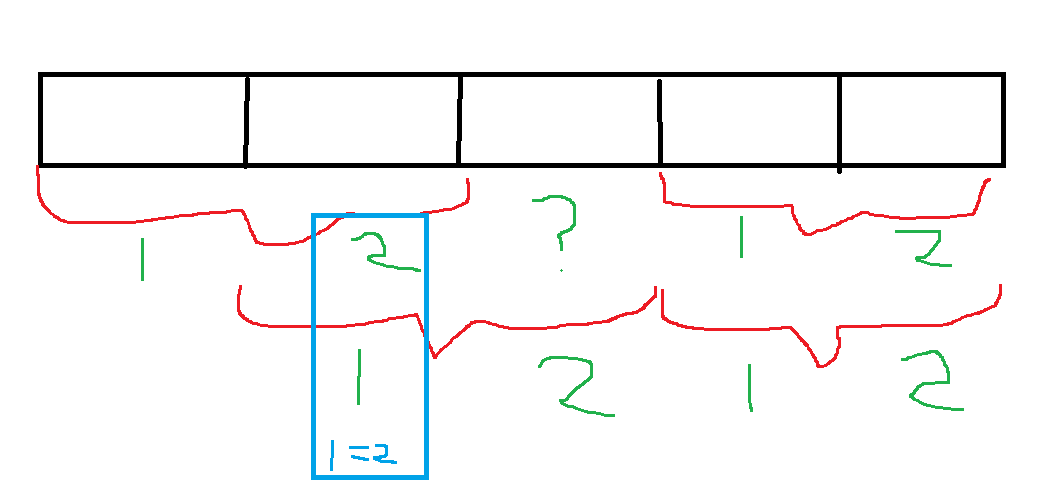
先查前后两大块，再将第一大块错开一位查询，可以发现两个查询都返回相同时，每一块区间都是相同的。

那么对 n 质因数分解，可知复杂度为 $O(2\log n)$ 级别，可以通过本题。