Codeforces Round #706 (Div. 2) A ~ F题解

D、E套路题。。

A. Split it!

左扫右扫判断一下就没了。

一开始有 n 个不同的数，令 $a = \operatorname{mex}\{a_i\},b = \max\{a_i\}$ ，每次加 $\lceil \frac{a+b}{2}\rceil$ ，加 k 次，问最后集合里有几种数。

一开始猜了个结论（显然只要集合里的数重复了1次，那么就会一直重复加该数），直接暴力模拟，结果t了。

打了下表，对于从零开始的连续数列每次会加进最大数+1的数。那么直接n+k就行。

对于不连续的数列，直接暴力模拟即可。

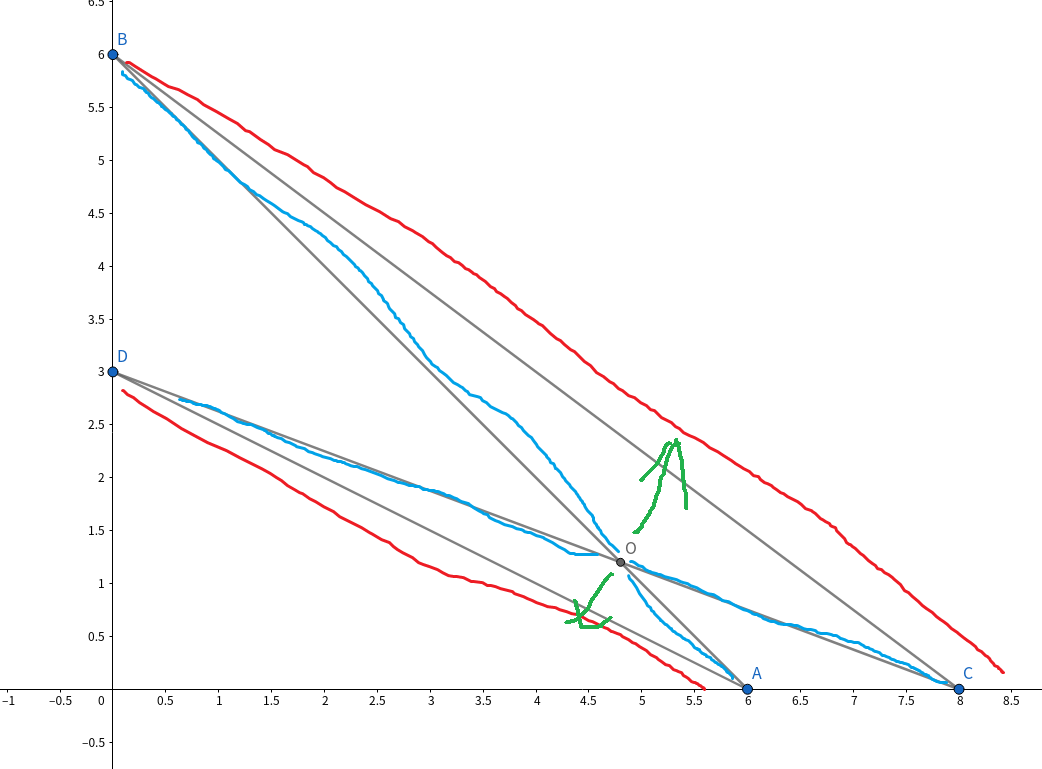
对于一个交叉的两条边，利用两边和大于第三边的三角不等式，推出不相交的更优。

整体的话，即从最上/最右侧的点开始匹配，总长度最小。

这道题，直接左扫右扫分类讨论一波就没了。

这题，构造很套路了。。

注意细节。

由于是边权为1的图，先 $O(n^2)$ 求出两点最短距离。

枚举两个点，考虑两个点的bfs生成树是否存在。

那么先考虑两个点最短路径是否唯一时会怎样。

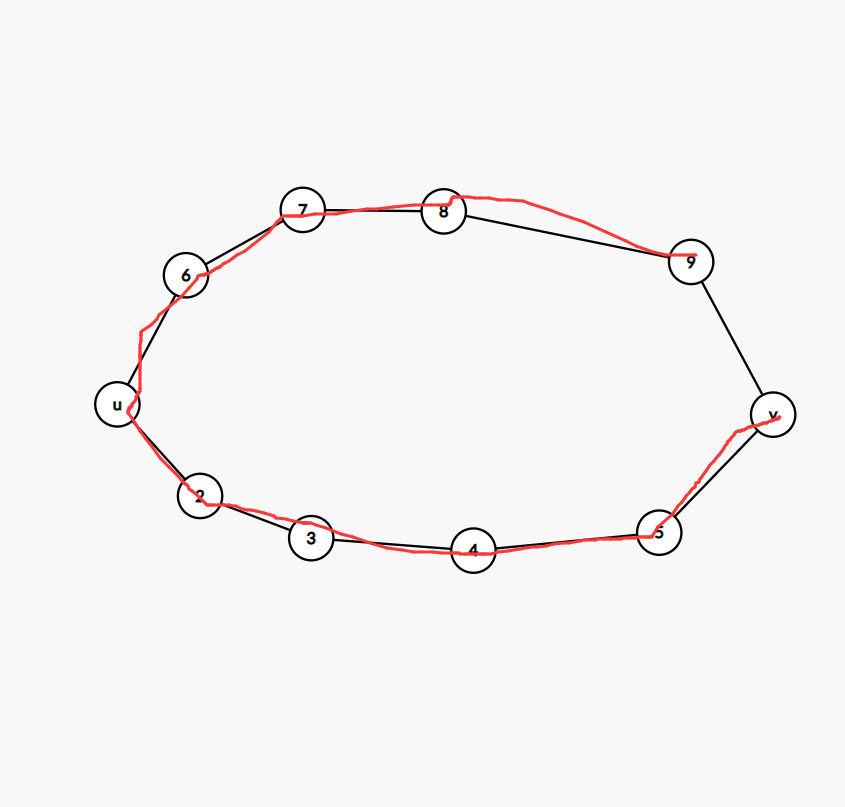
可以发现，不唯一时，bfs生成树必不会以u,v两个同时为根。

那么当最短路唯一，考虑不在最短路径上，其他点u的贡献。

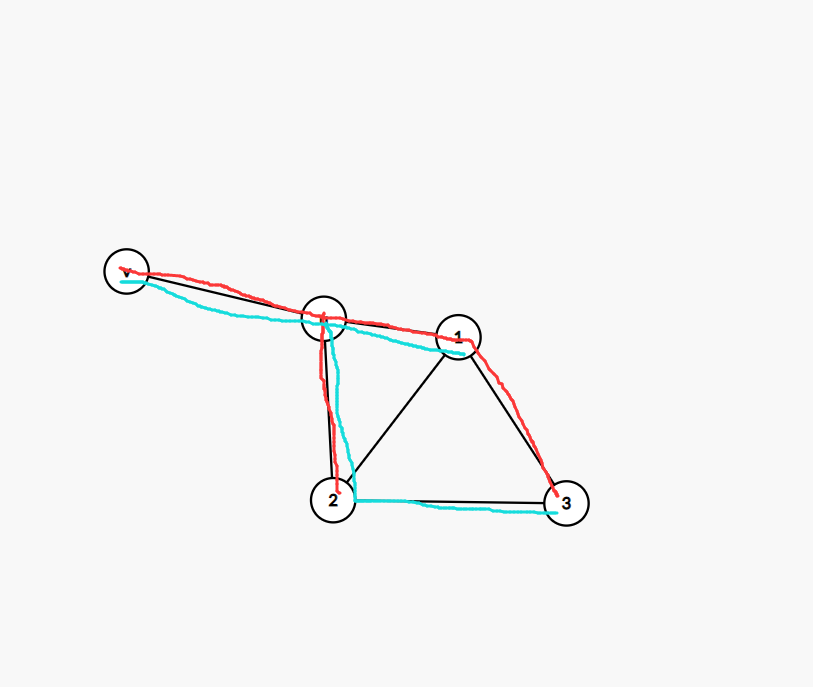
对于图中的u,v，显然有两个bfs生成树。那么除去u，v，每个点都要被从u，v延伸出的bfs生成树拉一条边连起来。

对于一个点x，枚举已经在bfs生成树内的点y（即相对于x，y距离 u,v 的bfs距离更近），看有多少个y（记作cnt）在原图满足

\begin{aligned} & d[u][x] = d[u][y] + 1 \\ & d[v][x] = d[v][y] + 1 \end{aligned}

那么对于一个点u就有cnt种选择。同一层距离层的点彼此独立（毕竟彼此不能连边），根据乘法法则，每个点对于答案的贡献为 $ans = ans * cnt$ 。

复杂度为 $O(n^2 m)$ 。