Codeforces Round #707 (Div. 2, based on Moscow Open Olympiad in Informatics) A ~ D 题解

A. Alexey and Train

模拟一下就行了。

平衡树 or set 判掉被浇到的饼就好了。

当出现四对 $a_i,a_j = S$ ，那么一定能找到两对和为 S ，且 4 个两两下标不同。

证明：把两个数 $a_i,a_j$ 合为 S 的连一条边。

当四对形式为 $(x,y_1),(x,y_2),(x,y_3),(x,y_4)$ ，图为

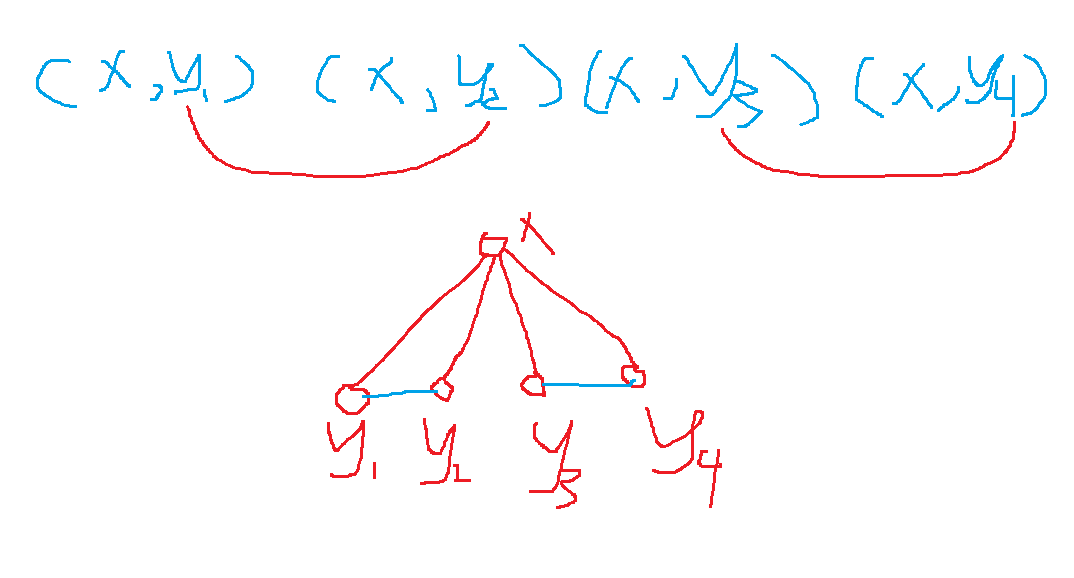
可以发现 $y_1 = y_2, y_3 = y_4$ ，那么 $(y_1,y_2),(y_3,y_4)$ 即为一组合法方案。

当四对形式为如图：

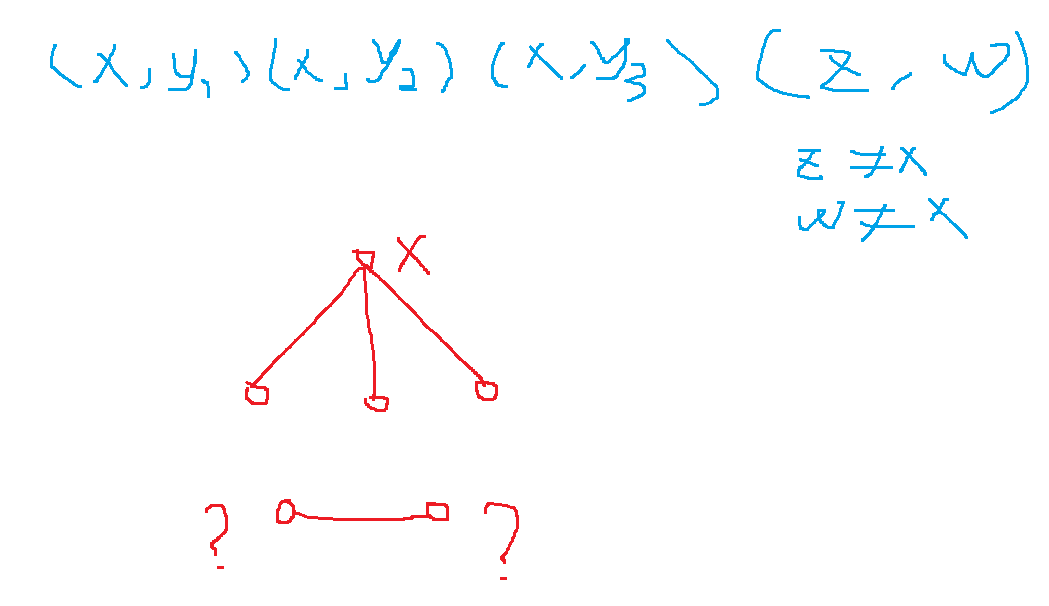
那么至少一个 $y_i$ 同时不等于 z,w ，那么就能找一对 $(x,y_i),(z,w)$ 。

除了上面两种形式，那么剩下的图，每个点的度，不超过 2 。那么明显 4 对必能找到两对构成合法的方案。

这有啥用呢？

两数之和的值域是 $C \in [2,6e6]$ 级别。那么每遍历一对 $a_i,a_j$ ，对应的 S 出现次数 +1 。当 $S$ 出现次数大于3，就说明必有一种方案。所以最多会遍历 $O(3C)$ 次。所以复杂度就为 $O(\min(n^2,C))$ 。

这道题其实很容易。

显然可以二分。只需要总天数减去颜色相同的天数即可。

由于每个数，至多在一个序列出现一次，那么记录 a 序列中 i 位置出现元素在 b 序列出现的位置 j （没有则跳过）那么对于一种颜色，减去的位置满足：

pos \equiv i(\bmod n) \\ pos \equiv j(\bmod m)

这个用EXCRT做就完事了。